分享给高三学生的六道值得一做的数学题目

　　

　　继续看题刷题选题分享题目，今日份题目如下：

　　

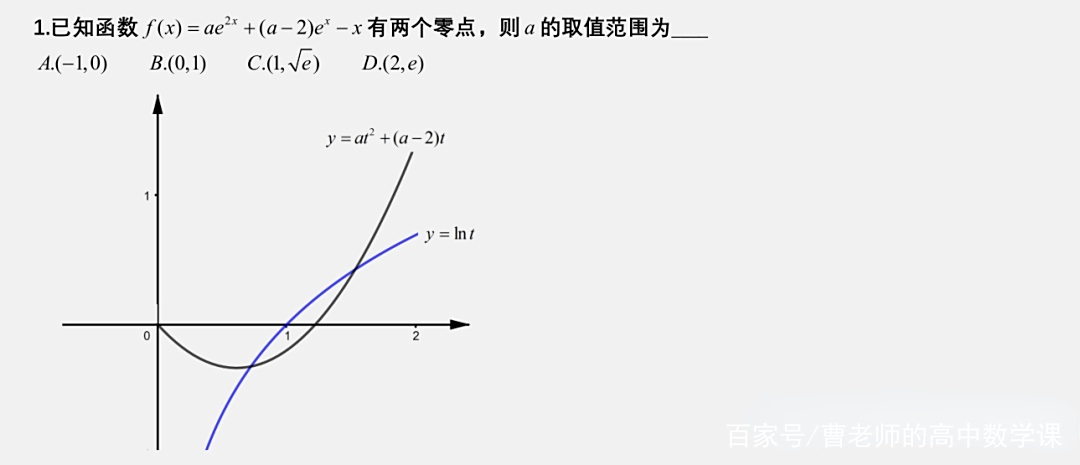
　　分析：原题无图，本题是最近某地高三文理试卷的第12题，由于是小题就没必要按照导数大题中零点问题的处理方法，用图像的交点个数来处理即可，将指数换元，转化为含参二次函数和对数函数的交点个数。

　　由于题目是单选，二次函数过原点，开口朝下时不可能有两个交点，当开口朝上时根据两函数的图像趋势只需令另外一个非零零点大于1即可，因此0<a<1很容易确定出来，或者直接利用两函数相切时确定出a的临界值，根据两函数的在临界值时的图像高低即可求出a的范围。

　　

　　

　　分析：题目是填空题的压轴题，解题时统一形式可把指数转化为对数，上下两式相加即可得到αβ的形式，但此时等式右侧虽并非严格αβ的形式，但也可直接将答案猜出来，这样做反而简单。由于题目中α,β独立，这种形式常见于指对数构造函数比大小的题目中，因此试着将两个式子用同一个函数表示，指数转化为对数后为lnα=3-α,将右侧式子整体取对数，将lnβ-1作为变量后可看出构造的式子为y=lnx-3+x，函数单调，因此α=lnβ-1，结合lnα=3-α即可求出αβ，这个题目构造函数的思路很容易想到，但构造函数并不容易看得出来。

　　

　　

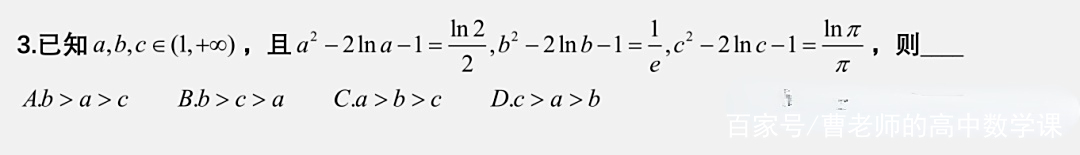
　　分析：这个题目是一个学生在后台提出的问题，思路很清晰，先比较等式右侧三个数的大小关系，显然三个数均满足函数y=lnx/x，函数在x=e处取得最大值，但x=2和x=π并不在同一个单调区间，怎么判断？既然不在同一个单调区间，那就变形后放到同一个单调区间内就可以了，ln2/2=ln4/4，这样三个数均在同一单调减区间，再根据单调性判断左侧函数的增减性即可。

　　

　　

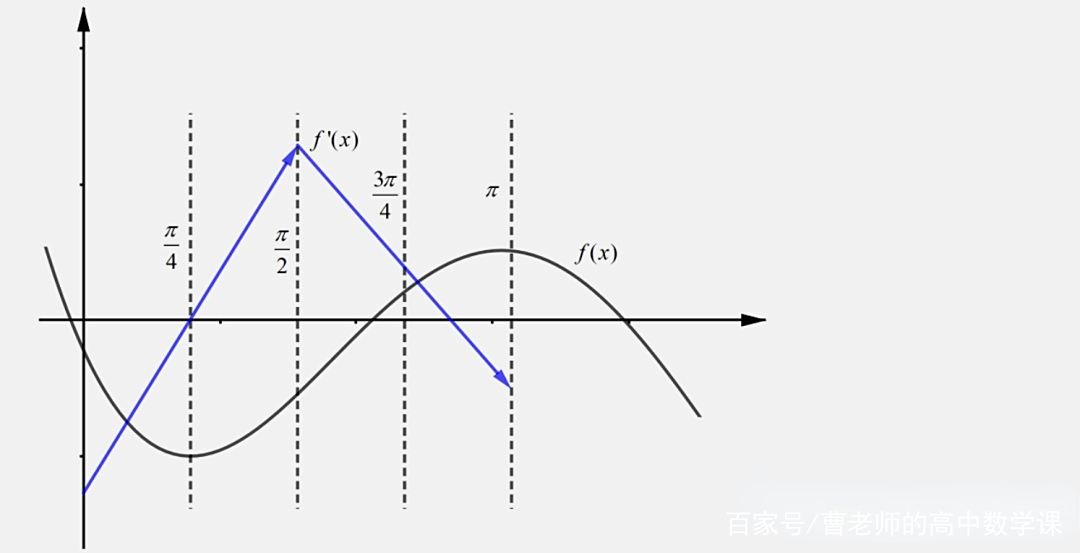
　　分析：题目是多选压轴题，该题本来是一道导数压轴大题，建议做这道题目的时候仍旧用大题的步骤来做，第一问a=1很容易判断，题目较难的部分是判断函数f(x)的增减趋势，这种题目的处理思路无非是切分区间和放缩，放缩这里并不单指的切线放缩，由于三角函数具有有界性，在特定区间内有上下界，通过上下界即可判断某些式子整体的正负，题目处理起来并不难，判断f(x0)<1时用到了隐零点法，过程如下：

　　

　　原函数图像和对应导函数趋势图像如下：

　　

　　

　　分析：这是最近看到的一个很不错的数列题，小题有小题的解法，作为小题难度不大，但如果题目设置成大题，则步骤的完整性就是一个重要考点了，最接近cn的整数并不能通过Sn-Tn的表达式直接看出，除非能证明出Sn-Tn是处在(k,k+)还是(k-,k)之间，下面的步骤自己参阅即可，明白大致思路之后怎么写都行，但在小题中直接根据Sn-Tn的表达式写出前几项找规律即可。

　　

　　

　　

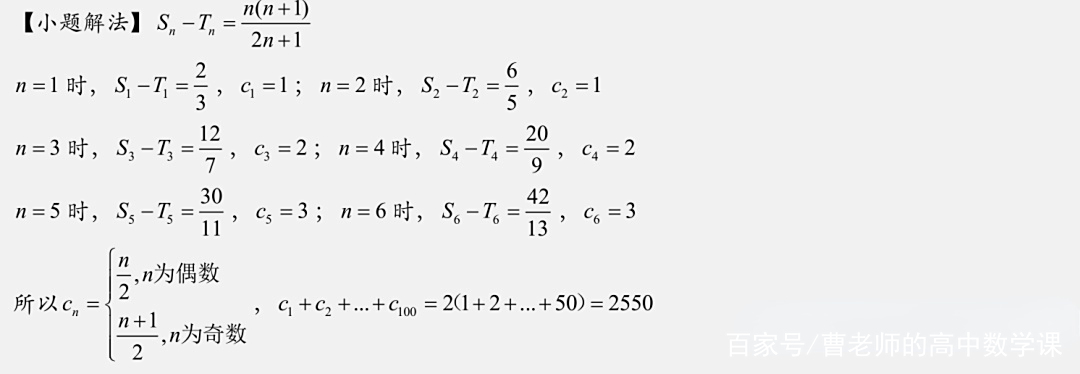
　　分析：建议不要看下面的解析，自己做一下第二问，看会采取哪些方法。

　　题目第二问中很奇怪的部分是不等式右侧又给了一项e^a，这跟不等式左侧中可以直接消掉，但为什么出题人多此一举？是不是说明不等式左右两个可以表示为同一函数下的不同变量表达形式？右侧x-a-2按照左侧的形式可拆分成x-1-(a+1)，若把e^(x-1)看作左侧的x，则右侧恰好为f(e^(x-1))，根据e^(x-1)>x，可知只需令函数f(x)在x>1单调递增即可，这个题目本没什么可说的，但不知道你在做题的时候能不能看得到这些不合理却又存在巧合的地方。